MATLAB ORTAMINDA PARÇACIK SÜRÜ OPTİMİZASYONU ÖRNEĞİ

 

1. Aşama: Başlangıç popülasyonunun oluşturulması

Yukarıda oluşan popülasyonda ssize satır sayısını, d ise sütun sayısını ifade eder.

2. Aşama: Başlangıç popülasyonlarının amaç (uygunluk) değerlerinin hesaplanması

3. Aşama: Parçacık ve sürü en iyi değerlerinin iterasyon boyunca güncellenmesi

Dikkat edilirse sürü içerisinde en düşük uygunluk değerine sahip çözüm (PSO literatüründe parçacık) find komutu bulunmuştur. Dolayısıyla en düşük değerine sahip çözüm (sürüde en iyi değere sahip parçacık) 4. çözümdür.

En iyi değere sahip parçacık, sürüdeki en iyi konuma sahiptir. (İlk iterasyon sonucudur.)

4. Aşama: Hız güncellemesi

Formüle ilk hızın katsayısı olacak şekilde w:eylemsizlik katsayısı da eşlik edebilir. c1 katsayısı bilişsel katsayı, c2 katsayısı ise sosyal katsayı olarak adlandırılır. Formülden çıkarılması gereken sonuç şudur:

Parçacık, hız güncellemesi yaparken önce ilk hızını korur, sonra kendisinin en iyi konumu ile arasındaki mesafeyi ardından da sürüdeki en iyi konum ile arasındaki mesafeyi kapatmaya çalışılır. Bu şekilde hızını artırmayı hedefler.

Kodlamada hız güncellemesi for döngüsü ile gerçekleştirilmiş ve her parçacığın hızı aşağıda verildiği gibi güncellenmiştir.

En düşük uygunluk değerine sahip parçacık, 4. parçacıktır. Ayrıca dikkat edilirse 4. parçacığın ilk iterasyondaki hız güncellemesi sıfır(0) şeklinde gerçekleşmiştir. Ancak diğer parçacıklardan bazılarının hızı artmışken bazılarının ise azalmıştır. Bu durumu şu şekilde açıklayabiliriz:

Başlangıç popülasyonunda hızlar zeros komutu ile sıfırdan başlatılmıştır. Dolayısıyla tüm parçacıkların ilk hızı sıfır ve en iyi konumları da mevcut konumlarıdır, hız değişiminin sebebi uygunluk değerlerinin minimize olmamasıdır. Minimize olmayan bir uygunluk değerinin (en iyi değere sahip olmayan parçacık) hız değişimine etki “c2 katsayısına sahip bileşen”den gelir. Çünkü uygunluk değeri minimal olmayan bu parçacıklardan hiç birisi sürü içerisinde en iyi konuma sahip değildir.

Yukarıda görülen hız güncelleme matrisinde, alt ve üst sınırların dışına taşan değerler görülmektedir. Arama sahasının hıza bağlı genişlemesi, global aramanın sağlanmasının rassal gerçekleşmesine neden olur, bu da algoritma mantığı ile çelişen bir durumdur. Bu nedenle, hız değerlerinin belirli bir aralıkta kalması sağlanmalıdır. Bu aralık da her satır ve sütunda; alt ve üst sınırlarına bağlı olarak örneğimizde -10 ile +10 arasında olmuştur.

Yeni hız güncelleme matrisi şu şekildedir: Görüldüğü gibi hız aralığını aşan değerler, +10 ve -10 değerlerinde sabitlenmiştir.

5. Aşama: Pozisyon güncellemesi yapılırken parçacığın sürü içerisindeki mevcut konumuna hız güncellemesi sonucu oluşan hız değeri ile birim zaman çarpımı eklenir, birim zaman değerce 1 olarak alındığı için; yeni konum, mevcut konuma yeni hızın eklenmesi ile bulunur.

İlk Konum Değerleri:

Son Hız Güncellemesi:

Güncelleme Sonrası Oluşan Yeni Konum = İlk Konum + Son Hız:

Hız güncellemesinde olduğu gibi iterasyon boyunca pozisyon güncellemesinde alt ve üst sınır değerleri aşılabilir, bu durumun da önüne geçilmelidir:

6. Aşama: Her parçacığın her iterasyon sonunda sürüdeki en iyi değer ve en iyi konumunun belirlenmesi sağlanmalıdır. Bunun için sürüdeki ilk değerler ile iterasyon sonunda elde edilen son değerler karşılaştırılır; minimizasyonun sağlandığı değer hangi parçacığa ait ise o parçacık sürüdeki en iyi konumuna ulaşır.

7. Aşama: Her parçacık sürüdeki en iyi konuma sahip olabilmek için çaba göstermektedir, ancak bu mücadelenin sonunda bir parçacık galip gelir ve sürüdeki en iyi konumuna ulaşır. Bu aşamada sürünün en iyisini bulmalıyız.

Her iterasyon sonunda en düşük uygunluk değerine sahip parçacık sürünün en iyi değerine sahip olur ve sürüdeki en iyi konuma ulaşır.

Kodlama sonucunda çıktı olarak sürüdeki en iyi konum ve sürüdeki en iyi değer alınır ve 50. iterasyon sonunda elde edilen sonuçlar şu şekilde gerçekleşir:

İterasyon boyunca uygunluk değerlerinde yaşanan iyileşmeleri ve ilerlemeleri her iterasyon sonunda gözlemleyebilmek için de amacit fonksiyonu kullanılabilir.

Görüldüğü gibi sürüdeki en iyi konuma sahip parçacığın uygunluk değeri ilk iterasyon başından yani 163,2169 değerinden, 50. iterasyon sonuna yani 1,9034’e kadar minimize edilmiştir.

Faydalı olması dileğiyle…

LinkedIn: www.linkedin.com/in/onurbagdat

MATLAB ORTAMINDA GENETİK ALGORİTMA METODU İLE OPTİMİZASYON ÖRNEĞİ

MATLAB ORTAMINDA GENETİK ALGORİTMA METODU İLE OPTİMİZASYON ÖRNEĞİ 

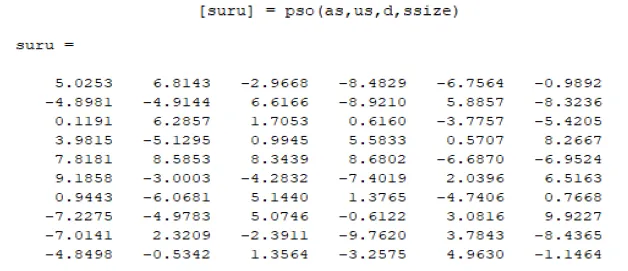
1. Aşama: Başlangıç popülasyonunun oluşturulması ile kodlamaya başlanır ve popülasyonda yer alan kromozomların uygunluk değerleri hesaplanır.

2. Aşama: Doğal seçilimin uygulanır ve bu seçilim sonucunda hayatta kalan bireyler belirlenir. (Bu aşamada rulet çarkı yöntemi kullanılmıştır, rulet çarkında yönteminde hedef maksimizasyondur; ancak çalışmamızda hedef minimizasyon olduğu için uygunluk değerlerinin çarpmaya göre tersi alınmıştır.)

Görüldüğü gibi uygunluk değeri en düşük olan kromozomun olasılığı en yüksektir. Rulet çarkı tekniğinde birikimli olasılıktan faydalanacağımız için, her kromozomun olasılığının bir önceki kromozomun olasılığı ile toplanması gerekir.

Hangi kromozomun hayatta kalacağının belirlenmesi için atanan rastsal değerin birikimli olasılıktan küçük olduğu ilk kromozomun tespit edilmesi gerekir.

Gerçekleştirilen doğal seçilimin sonucu oluşan ara popülasyon aşağıda görülmektedir: Bu sonuca göre 1. kromozomdan iki adet, 2. kromozomdan bir adet, 4. kromozomdan ise yine bir adet ara popülasyonda yerini almaktadır. En iyi uygunluk değerine sahip 3. kromozom ara popülasyonda yer bulamamıştır. Ancak iterasyon sayısı arttıkça en uygun kromozomun hayatta kalma olasılığının artacağı da unutulmamalıdır. Not: Genetik Algoritmada doğal seçilimden çıkan ara popülasyon, ebeveynlere karşılık gelmektedir.

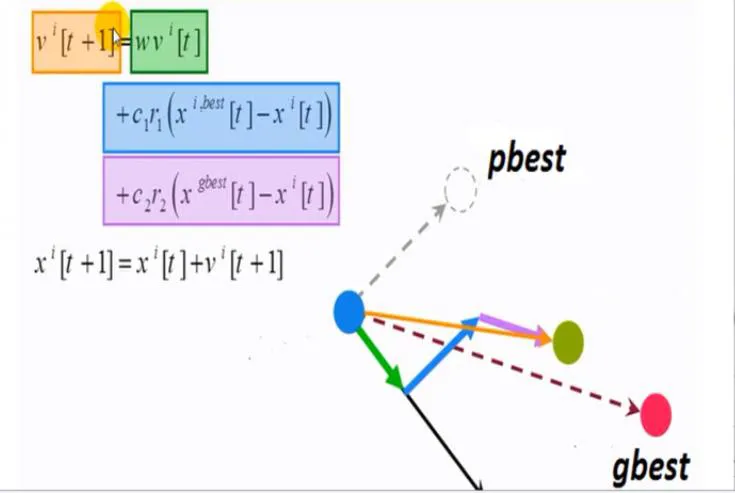
3. Aşama: Çarprazlanacak çiftlerin belirlenir, bunun için tek noktadan veya çift noktadan gen transferi gerçekleştirilebilir.

Çarprazlanacak çiftler belirlendikten sonra çarprazlama noktası belirlenir ve kromozomlar arasında karşılıklı gen alışverişi sağlanır.

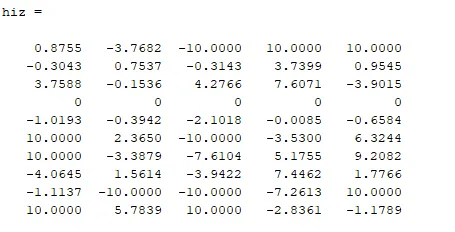
Çarprazlama sonucu oluşan ara popülasyon aşağıdaki gibidir. Görüldüğü gibi, 2. ve 3. Kromozomlar aralarında çarprazlama gerçekleşmiştir. 

NOT: Genetik Algoritmada çarprazlamadan çıkan ara popülasyon, çocuklara karşılık gelmektedir.

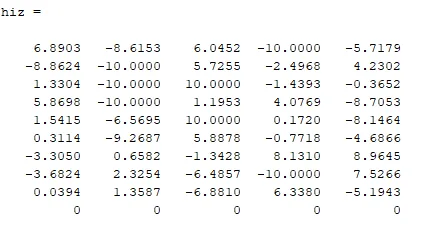
4. Aşama: Çarprazlama sonucunda oluşan ara popülasyonda yaşanabilecek mutasyonu tespit ederken değer bazlı bir kodlama gerçekleştirilir. Öncelikle ara popülasyonun satır ve sütun sayıları ile aynı formda bir rassal sayı atanır ve gen başına düşen mutasyon olasılıkları dikkate alınır. Mutasyon olasılığı 0.001 ile 0.1 arasında değişmektedir. Rassal sayı atandıktan sonra gen gen inceleme yapılır ve mutasyon olasılığından düşük olan gen mutasyona uğrayacaktır.

Ardından her satır ve sütun için yapılan mutasyon olasılığı incelemesi sonucunda mutasyona uğrayacak gen için (rassal sayı)*(komşuluk payı)*(aralık) işlemi neticesinde mutasyon gerçekleştirilir.

5. Aşama: Yeni neslin belirlenmesi için belirli bir iterasyon süreci boyunca hem en uygun amaç fonksiyonu değeri hem de bu değeri sağlayan çözüm(yani:satır) tespit edilmelidir.

6. Aşama: En iyi çözüm satırı (yani en optimize kromozom) ve bu en iyi çözüme karşılık gelen en iyi değer (yani kromozomun optimize uygunluk değeri) iterasyon boyunca bulunur ve tespit edilir.

SONUÇ: Problem boyutu (psize:satır sayısı) ve değişken sayısına (d:sütun sayısı) bağlı olarak oluşan en iyi çözüm ve en iyi değer sonuçları aşağıda görüldüğü gibidir.

Faydası olması dileğiyle…

LinkedIn: www.linkedin.com/in/onurbağdat

https://www.youtube.com/channel/UCFwypXAxZScWxb7St8xWh9g